

Random Sampling Neural Network for Quantum Many-Body Problem
Introduction:
The eigenvalue problem of quantum many-body systems is a fundamental and challenging subject in condensed matter physics, since the dimension of the Hilbert space (and hence the required computational memory and time) grows exponentially as the system size increases. A few numerical methods have been developed for some specific systems, but may not be applicable in others. Here we propose a general numerical method, Random Sampling Neural Networks (RSNN), to utilize the pattern recognition technique for the random sampling matrix elements of an interacting many-body system via a self-supervised learning approach. Several exactly solvable 1D models, including Ising model with transverse field, Fermi-Hubbard model, and spin-1/2 XXZ model, are used to test the applicability of RSNN. Pretty high accuracy of energy spectrum, magnetization and critical exponents etc. can be obtained within the strongly correlated regime or near the quantum phase transition point, even the corresponding RSNN models are trained in the weakly interacting regime. The required computation time scales linearly to the system size. Our results demonstrate that it is possible to combine the existing numerical methods for the training process and RSNN to explore quantum many-body problems in a much wider parameter regime, even for strongly correlated systems.
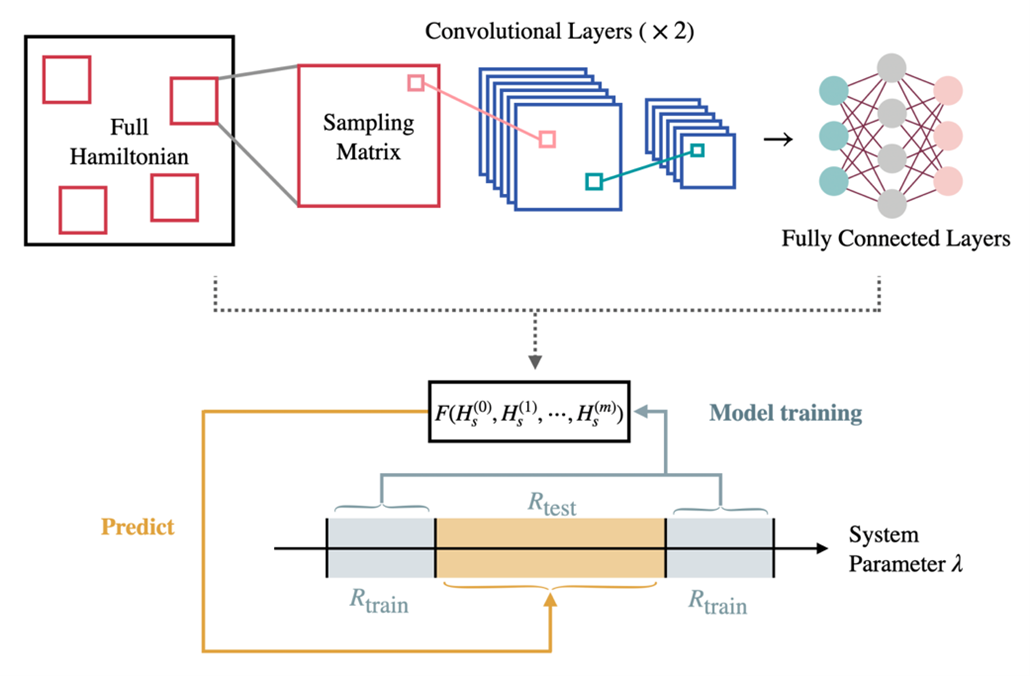
(Caption) A typical flowchart of a RSNN model. The input data are M × M matrices, randomly sampled from the original full system Hamiltonian (see the text). After a standard self-supervised learning by a CNN model with known results in the training regime (R train), the obtained RSNN model can be used to predict physical results in the test regime (R test). In most physical problems, the training and test regimes can be defined by a continuous system parameter.
The corresponding loss function during the training process is designed as :
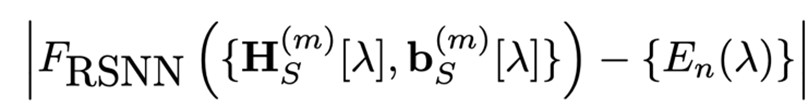
In order to demonstrate the applicability of RSNN, we first take 1D spin-1/2 Ising Model with a Transverse Field (IMTF) [1] as an example for systematic studies. The system Hamiltonian is known to be:
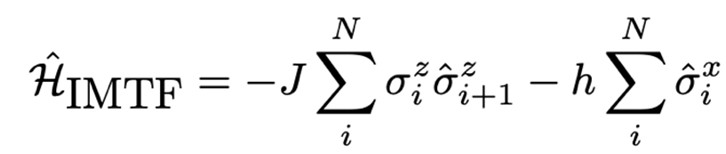
1D IMTF with the periodic boundary condition is known exactly solvable though the Jordan-Wigner transformation, and therefore could be a good example to test the application of our RSNN. In the thermodynamic limit, the ground state is a double degenerate ferromagnetic phase as h < J, and becomes a non-degenerate paramagnetic phase as h > J.
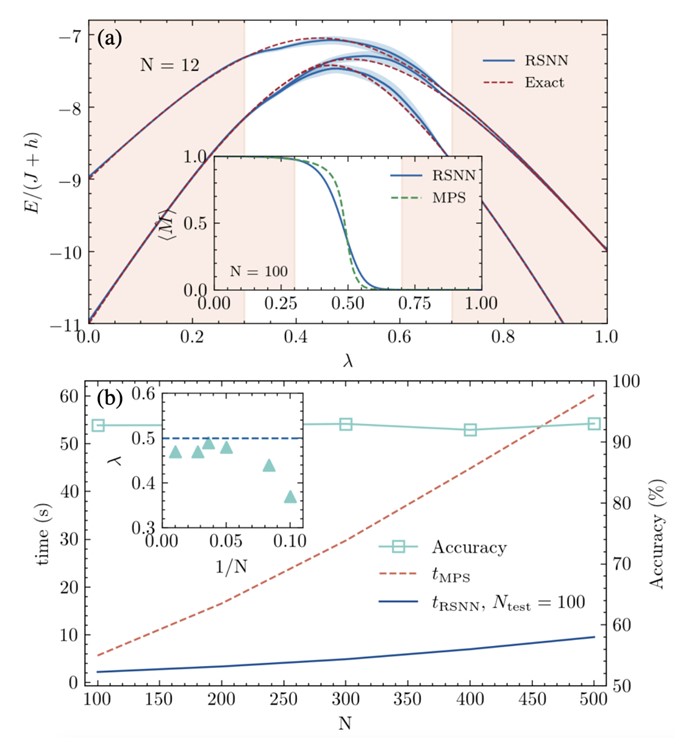
(Caption) (a) Prediction result of the lowest three eigenenergies of 1D IMTF by RSNN (solid lines) for N = 12. The training regime, R train = (0, 0.3) ∪ (0.7, 1.0), is shown by the colored background, and the test regime, R test = (0.3, 0.7) is by the white background. The blue gray area near the RSNN result indicates the uncertainty, resulting from five independent calculations. The results obtained by the exact diagonalization (dashed lines) are shown together for comparison. The inset shows the predicted magnetization (solid line) for N = 30, compared to the results obtained by MPS (dashed line). Here we use N train = 10000, NS = 200, and M = 10 for the training process (see the text). Note that we have scaled the energy in unit of J +h in order provide a more balanced expression of eigenstate energies in the training regime. (b) shows the average computation time (solid line) to generate a test data by RSNN for N test = 100 data points (see the text). The computation time by MPS (dashed lines) as a function of system sizes are also shown together for comparison. Accuracy of the magnetization of RSNN method are also shown together by open squares. The inset shows the finite size scaling of the phase transition point, which is defined when the separation between the lowest two eigenenergies is larger than their uncertainties. Horizontal dashed line is the quantum critical point (lambda c = 0.5) in the thermodynamic limit. Other parameters are the same as (a).
In order to investigate the application of RSNN in the strongly correlated regime, here we consider 1D Fermi-Hubbard model (1D FHM) with the following system Hamiltonian:
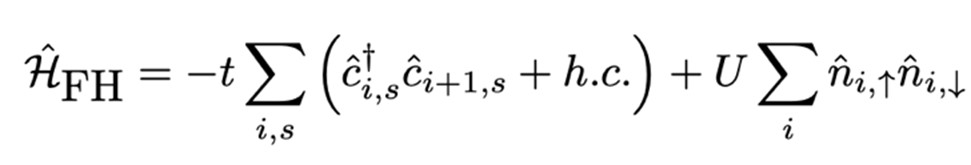
For simplicity, here we just consider the energy spectrum of holon excitations in the charge sector.
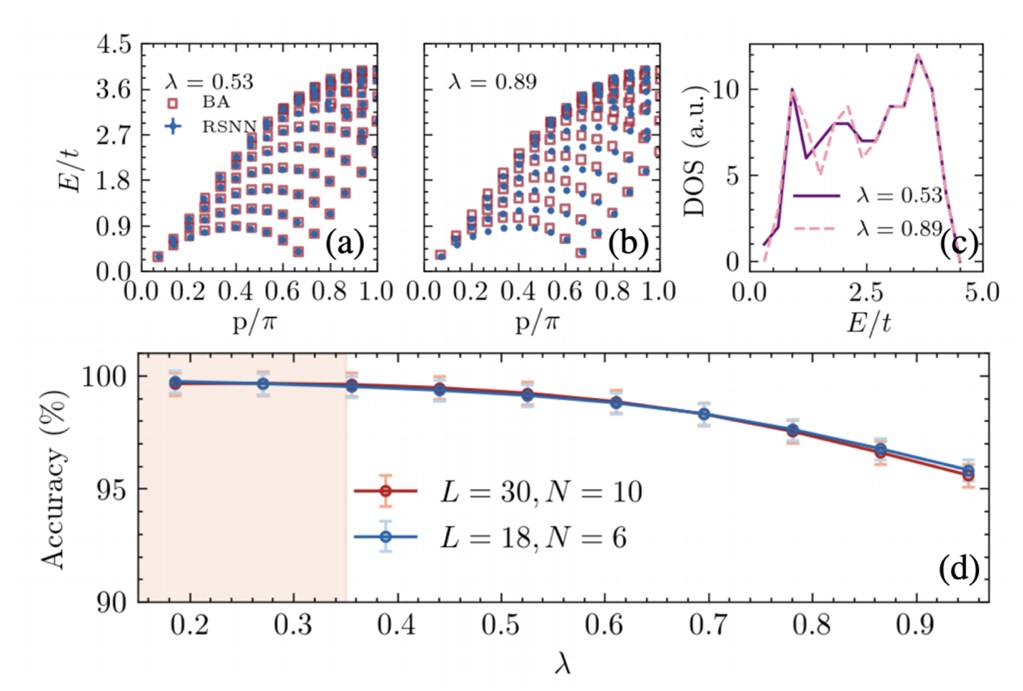
(Caption) (a) and (b) are predicted holon excitation spectrum (blue dots) of 1D FHM by RSNN for \lambda ≡ U/(t+U) = 0.53 and 0.89 respectively. The training regime is R train = (0.1, 0.35) with L = 30, N = 10 and N↓ = 5. Exact results calculated by Bethe-ansatz (BA, red open squares) are also shown together for comparison. (c) shows the associate density of states (DOS) obtained by RSNN. (d) shows the accuracy of the energy spectrum with an uncertainty by RSNN in the test regime, R test = (0.35, 1.0) (white background). Results for two different system sizes are shown together for comparison.
We note that it is still impressive that the accuracy can be still larger than 95% even for U/t ∼ 12, showing that RSNN could be a very promising tool to estimate physical quantities in a strongly correlated system even it is trained in the weakly interacting regime.
One of the most important advantages of RSNN is that one just needs to train the model one time in the training regime and then gets an arbitrary amount of data immediately in the test regime, even in the strongly correlated regime or near the quantum phase transition point. Combination of RSNN with other numerical methods may provide a very effective approach to explore quantum many-body problems.
Publication and AI model:
Random Sampling Neural Network for Quantum Many-Body Problems, Chen-Yu Liu and Daw-Wei Wang, arXiv: 2011.05199 (2020).
We also provide Github code for the application of RSNN in 1D Ising Model with a Transverse Field:
https://github.com/ CYLphysics/RSNN_TFIM1D
Research Team:
©copyright Artificial Intelligence for Fundamental Research (AIFR) Group